最佳化的另一種用法（Overfitting簡易偵測）

最佳化Overfitting簡易偵測

• 參數不平滑（尖尖），一定容易有Overfitting的問題（或統計上顯著性不足）
• 參數平滑相對安全，但未必一定沒有Overfitting的問題

請注意，最佳化的Overfitting偵測只能證明容易有，但不能證明一定沒有，若要再進一步檢驗是否仍有Overfitting嫌疑，則要改用Out-of-Sample Testing或WFO

實例說明

以上面這個最佳化3D圖為例，請檢視圖中兩個圈圈的區域

• 紅色圈圈的尖尖區域一定容易有Overfitting的問題（統計上的顯著性不足）
• 綠色圈圈較平滑的區域則相對安全（但未必一定沒有Overfitting的問題）

為了進一步證明紅色圈圈的尖尖區域存在Overfitting問題，以下用WFO來檢視此兩圈圈區域的OOS(Out-of-Sample)的Robustness與OOS的績效

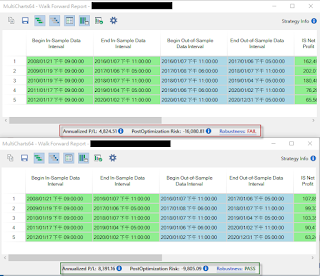
上圖為兩個WFO測試的結果，可以看到這兩個WFO使用相同的資料並且IS (In-Sample)與OOS也使用相同的時間區段，所以是個公平的檢測

上半邊代表紅色圈圈組別，因為五個Run裡面有三個正好落在紅色圈圈的尖尖區域

• OOS的Robustness：沒過 (WFE = 47%)
• OOS的績效：低 = 0.30 (= 4,824.51 / -16,080.81 * -1)

下半邊代表綠色圈圈組別，因為五個Run全部落在綠色圈圈較平滑的區域附近

• OOS的Robustness：通過 (WFE = 80%)
• OOS的績效：高 = 0.86 (= 8,391.16 / -9805.09 * -1)

要讓策略Overfitting很容易，但要偵測出來卻沒那麼容易

所以研發策略時的每一步都要很小心

策略真的能賺的到錢，靠的是有效的統計，而非千錘百鍊的複雜程式邏輯